A Domain-Oblivious Approach for Learning Concise Representations of Filtered Topological Spaces for Clustering, Yu Qin et al., IEEE VIS (TVCG) 2021
The annual IEEE Visualization conference is happening this week, so let’s explore some papers in the conference this year! One paper that caught my attention is about topology, which is a heavily studied discipline in visualization. Topology in visualization is usually used as a data abstraction technique to quantify the differences between shapes, thus allowing operations such as clustering to group images based on their topological properties. However, one problem is that the data abstraction is in a form of Persistence Diagram (PD) (you can think of it as a scatter plot, where each dot represents the significance of an “edge/ connection/ circle…” in the shape). To quantify the difference between two shapes in terms of the PDs, we usually apply a metric called Wasserstein or Bottleneck distance. Such distance metric has a time complexity of \(O(n^2log^2n)\), which makes clustering of 10,000 images hard to be achieved in tractable time. Therefore, this work tries to make distance metric between PDs efficient by learning a hash function that converts the diagrams into bit vectors, such that the Hamming distance between the vectors (which can be efficiently computed with a XOR operation) are similar to the Bottleneck distance. The whole idea of learning such a hash function is based on Generative Adversarial Network (GAN), a deep learning technique commonly used in image generation and style transfer:
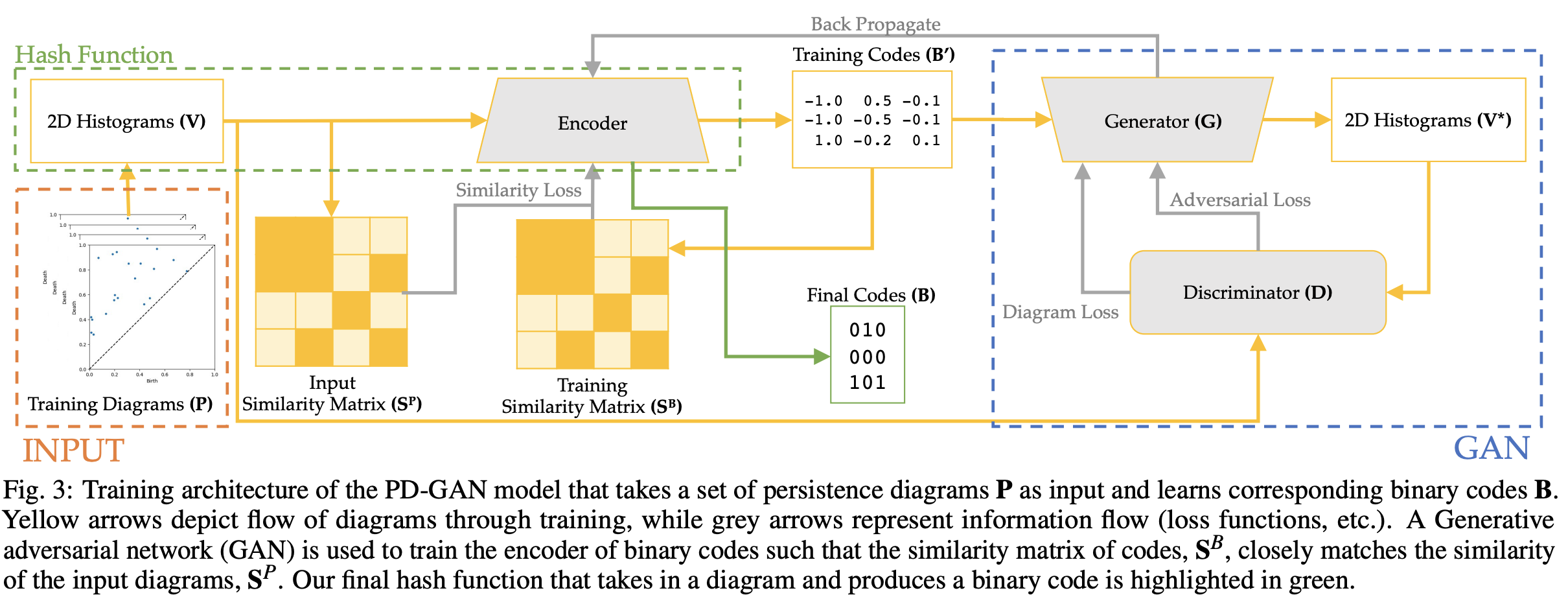
The whole pipeline first starts with aggregating each PD into a 2D histogram \(V\). Then, the pipeline consists of an encoder network (based on VGG19) and a GAN (generator and discriminator). The encoder generates codes from the PDs that are (1) real representations \(B'\) from output binary codes \(B\) so that they can construct a similarity matrix \(S^B\), and (2) inputs to the generator to recover the 2D histograms \(V^*\). The loss function consists of the differences between the true and generated similarity matrix (\(\|S^P - S^B\|\)), the real and binary representation of the codes (\(\|B - B'\|\)), the original and generated histograms (\(\|V - V^*\|\)), and the adversarial loss from GAN.
One surprising result from the experiment is that, the Persistence Diagrams used for training the hash function do not need to come from the original shapes or images. They could be any random scatter plots under a uniform persistence point distribution. Also, they only need to have number of points close to the average number of points per plot in the test data. This makes the hash function domain-oblivious, which means we do not need domain-specific training data. We can just generate synthetic data to achieve the same clustering goal.
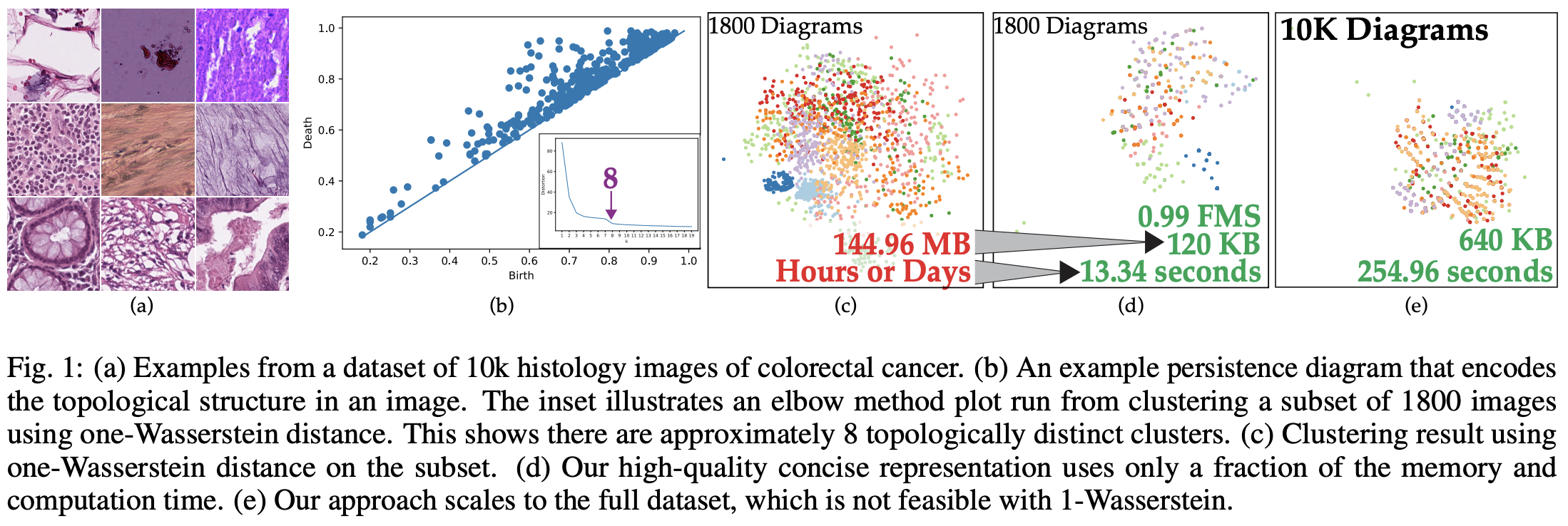
Here is an example of clustering 10k histology images of colorectal cancer using the trained hash function: